7. Exponential Functions
Resources for 7. Exponential Functions
| Site: | ARPDC |
| Course: | ERLCMath 30-1, 2012-2014 - Stephanie MacKay (Click to Enter) |
| Book: | 7. Exponential Functions |
| Printed by: | Guest user |
| Date: | Monday, 25 November 2024, 2:14 AM |
7. Exponential Functions
Exponential Functions Performance Task contributed by Debbie Terceros and Josie Nagtegaal.
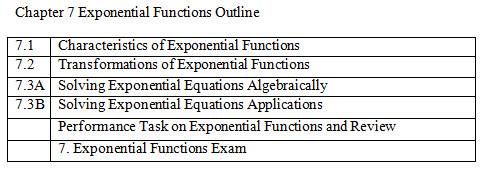
7.1 Characteristics of Exponential Functions
Class Notes
The McGraw-Hill Ryerson PreCalculus 12 Text is used as the Main Resource.
Assignments in the Powerpoint Lesson Plans refer to pages and questions in the PreCalculus 12 text.
7.1 Characteristics of Exponential Functions
Digital Resources to Enhance Learning and Differentiate Instruction
McGraw Hill Math 30-1 Teachers Resource DVD N04_7.1_338_AI Explore the effect of changing the base.
(Once downloaded, right mouse click and set to Open with Explorer.)
7.2 Transformations of Exponential Functions
Class Notes
The McGraw-Hill Ryerson PreCalculus 12 Text is used as the Main Resource.
Assignments in the Powerpoint Lesson Plans refer to pages and questions in the PreCalculus 12 text.
7.2 Transformations of Exponential Functions
Digital Resources to Enhance Learning and Differentiate Instruction
McGraw Hill Math 30-1 Teachers Resource DVD
N04_GG_v1 Geogebra file for Transformations
N05_7.2_348_IA Explore Parameters a and b
7.3 Solving Exponential Equations
Class Notes
The McGraw-Hill Ryerson PreCalculus 12 Text is used as the Main Resource.
Assignments in the Powerpoint Lesson Plans refer to pages and questions in the PreCalculus 12 text.
7.3A Solving Exponential Equations
7.3B Applications of Solving Exponential Equations
Pedagogical Shifts: TRANSFORM, Moving from Traditional to Student-centered
Shifting from content based to competencies based
Shifting from Student as Knowledge Recipient to Student as Inquirer and Creator
Shifting from Memorization to Higher-level Thinking
Shifting from One-size-fits-all to Personalized, Differentiated
Building and Solving Equations Activity Template
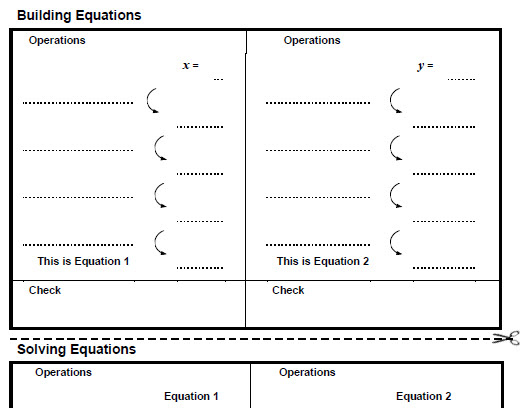
I used, this template as an introduction to Solving Exponential Equations. Students had to build exponential equations starting from x = #. For example, x = 3, In the next step, multiple by 2 to get 2x = 6. Add 3 to both sides, 2x+3 = 9. Finally raise each side of the equation to a base: 5^(2x+3) = 5^9. I had students switch papers and them solve the equation by undoing the steps in the reverse order. I liked how students were able to justify the strategy of equating the exponents when the bases are the same.
