Teaching Strategies
A collection of strategies intended to assist student learning.
| Site: | ARPDC |
| Course: | ERLC High School Mathematics Learning Community |
| Book: | Teaching Strategies |
| Printed by: | Guest user |
| Date: | Friday, 25 April 2025, 11:39 PM |
Board Work in Random Groups
Peter Liljedahl was the keynote speaker at two Alberta High School Math Institutes hosted by the ARPDC. His presentations included results from studies showing that student thinking and engagement is increased when students work on non-permanent vertical surfaces in random groups. View videos of his presentations on the ERLC site. (Presentation 1, Presentation 2)
What it looks like.
Present the class with a problem.
Make random groups and assign each group a section of the board to work at.
Monitor student progress and assist as needed. Promote discussion within and between groups.
After a satisfactory period of time ask students to return to their desks and debrief the activity using the work still on the boards.
The Benefits.
Promotes teaching each other and discussion which are key aspects of communication.
Ability to see students work and assess level of understanding.
It is harder for students to hide.
Creating movement and getting out of the desks adds energy to the class.
A vertical non-permanent surface for work encourages students to take risks and try things.
Random groups promotes a positive class atmosphere and gives the class an opportunity to get to know everyone.
The Challenges.
Not enough board space... try some groups on the board and some at their desks.
It takes some effort to encourage students to communicate well. Try telling students to take turns writing. To encourage this call out "switch" so that they have to change. A good rule to establish is that if you have an idea you are not allowed to write it down. You have to communicate it to a group member who can then write it down.
Think-Pair-Share
What it looks like.
A Think-Pair-Share involves students having individual "think time" about some topic or question, then they may discuss with a partner, and finally partners share their thoughts with the entire class.
M10-C Think-Pair-Share Example:
I presented the "What do you see?" slide below and asked my Math 10-C class to come up with as many mathematical things as they could.
We did a Think-Pair-Share and the combined results of our class brainstorming are shown below.
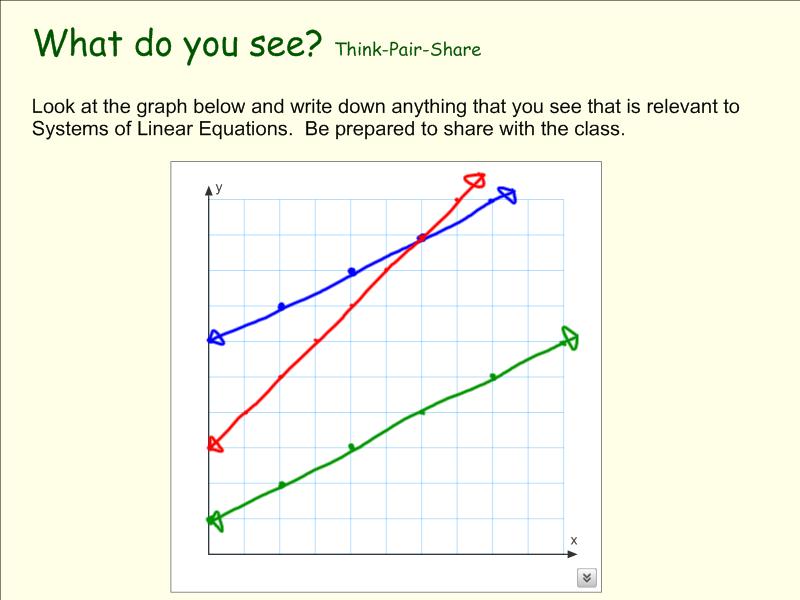

I had taught my class how to solve a system of linear equations graphically but we hadn't discussed the possible number of solutions to a system.
This Think-Pair-Share served as a great warmup to this topic and tied in nicely with the rest of the lesson.
Jig Saw Activity
What it looks like.
A Jig Saw involves students working on a problem individually, then collaborating with classmates to make sure they are experts on the problem, and finally teaching classmates how to solve the problem.
Students
... work on a problem individually,
... become experts on that problem by collaborating with classmates
... and then teach peers how to solve the problem.
Teachers
... choose 4 different problems and put one on each sheet of the Jig Saw Template.
... Make groups and make sure that expert groups have the correct solution before teaching peers.
Click here for a template to make a Jig Saw Activity. Student instructions included on template.
M20-2 Jig Saw Example:
This Jig Saw had students graph a quadratic function without technology and state the characteristics. Each separate problem was the same quadratic function but presented in a different form. When the students got back together they were surprised to see that everyone had the same graph and some great discussions were had related to the different strategies used based on the given form.
Jig Saw Quadratic Function Forms
Jig Saw Quadratic Function Forms KEY
The Benefits.
Promotes teaching each other and discussion which are key aspects of the process of communication.
This activity promotes understanding a problem very well. It takes some time but is useful for mastering major concepts.
Research Project

The Alberta Mathematics Curriculum includes a Mathematics Research Project for M20-2 and M30-2.
"Research and give a presentation on a historical / current event or an area of interest that involves mathematics. [C, CN, ME, PS, R, T, V]"
The following links provide resources from the Alberta Assessment Consortium designed to assist the implementation of these research projects.
Show Me You Know Assignment
What it looks like.
A "Show Me You Know..." Assignment involves the students providing evidence that they understand a particular concept. This evidence can come in various forms (written, audio, video, etc.). This type of assignment works well for procedural concepts and students demonstrate a "recipe" explaining the mathematical steps involved.
M10-C Systems of Linear Equations Example:
The following link contains two examples of student solutions to a "Show Me You Know... Substitution" Assignment.
Show Me You Know Substitution Example
Applying Assignments
What it looks like.
Students are presented with a number of problems that require them to apply their skills in a new context. Students will select a question and write a complete solution to the problem including all explanations of their thinking.
Marking will be done according to the rubric below that breaks up the mark into half for the solution and half for justification / communication.
M10-C Polynomials Example:
The file below is an example of an Applying Assignment for Algebra & Number in Math 10-C.
Algebra & Number Applying Assignment
Example to Show Students
Below is an example that may be used to help explain expectations.
Susan is making a rectangular area rug with a similar design to a square rug she made earlier. (MHR pg. 212)
a) What are the dimensions if the new rug is 2 ft longer and 1 ft narrower than the square rug?
b) Write an expression for the area of the new rug.
c) If the square rug is 3 ft by 3 ft, which rug has the greater area?
|
Poor Solution (5/10) |
Good Solution (10/10) - correct solution and clearly explained. |
Develop Relationships
The following strategies may be helpful in developing relationships with students and promoting a positive classroom atmosphere that is conducive to communication.
![]()
Who I Am Sheet
 |
Students fill out the sheet and return it to the teacher (the self portraits are usually the best!). This sheet can then be a nice way to start conversations with students. When there is time you can take out a students sheet and strike up a conversation about some of the items from their "Who I Am" handout. It is believed that this sheet originally came from Dan Meyer. Please click the image to download a pdf version. |
![]()
Five Things in a Bag
| The idea behind "Five Things in a Bag" is that students will have a set day when they are to bring in a bag with five items that show something about themselves and their interests. They will then show and explain these items to the class. It often works well to have the teacher demonstrate first and then set a schedule with a few students presenting on the same day. |  |
![]()
Commonalities and Uniquities
Compile a list of 6 things that students in your group have in common. Then try to find at least 2 uniquities for each person.

Row Games
|
What is a Row Game? A row game is a partnered activity where one student completes the exercises in column A while the partner completes the exercises in column B. In one version of the game, each column has a different question, however, the answers match. Students work on their question independently and compare answers. If the answers do not match, students must work together to discover and correct the error. In another version of the game, students may be asked to add their individual answers and compare to a sum presented in a third column. The Benefits of a Row Game Students are held accountable by each other and great discussions can be had when answers don't match and students try to figure out where the problem is. Links for Row Games A Google search for row games led me to Kate Nowak's blog and John Scammell's Orchestrated Experiences for High School Math. Each site contains an explanation of the process and benefit of row games and some sample row games to use.
|
 |
ARPDC Row Game Collection
Row games can be nice activities to use in class but take some effort to put together due to finding questions that have the same solution. It is my vision to use this page as a repository of row games that are matched to Alberta Curriculum. John Scammell has a start on this and hopefully all the teachers in Alberta enrolled in these demonstration courses can continue this work and build a nice organized resource of row games that may be used in high school mathematics.
If you have a row game to contribute please email me at colin.veldkamp@epsb.ca and I will organize them in the space below. The following templates may be useful when building a row game: Row Game - Template and Row Game - Sum Template.
| Mathematics 10-C |
|
Measurement RG - Volume Word Prblms (Nowak) Trigonometry RG - Right Triangle Trigonometry Linear Equations & Graphs RG - Slope Intercept Form (Nowak) Polynomials Final Review |
| Mathematics 20-1 |
| RG - Operations with Radicals |
| Mathematics 20-2 |
|
- |
| Mathematics 30-1 |
|
Relations & Functions Exponents & Logs RG - Exponential Equations (Scammell) Trigonometry |
| Mathematics 30-2 |
|
Rational Expressions & Equations Counting Methods |
| Mathematics 30-3 |
|
- |
