5. Trigonometric Functions and Graphs
5.2 Transformations of Sinusoidal Functions
Class Notes
The McGraw-Hill Ryerson PreCalculus 12 Text is used as the Main Resource.
Assignments in the Powerpoint Lesson Plans refer to pages and questions in the PreCalculus 12 text.
![]() 5.2 Transformations of Sinusoidal Functions
5.2 Transformations of Sinusoidal Functions
![]() 5.2 Formative Assessment Graphing Phase Shift and Displacement
5.2 Formative Assessment Graphing Phase Shift and Displacement
Digital Resources to Enhance Learning and Differentiate Instruction
Pedagogical Shifts: TRANSFORM, Moving from Traditional to Student-Centered
Shifting from Student as Knowledge Recipient to Student as Inquirer and Creator
Shifting from Memoriation to Higher-level Thinking
Shifting from competative to collaborative learning.

![]() Matching Sinusoidal Equations with Graphs and Properties
Matching Sinusoidal Equations with Graphs and Properties
In this activity, students worked in pairs to match the graph with the function equation and function table. They also had to list the features of the graph including amplitude, period, and principal axis.
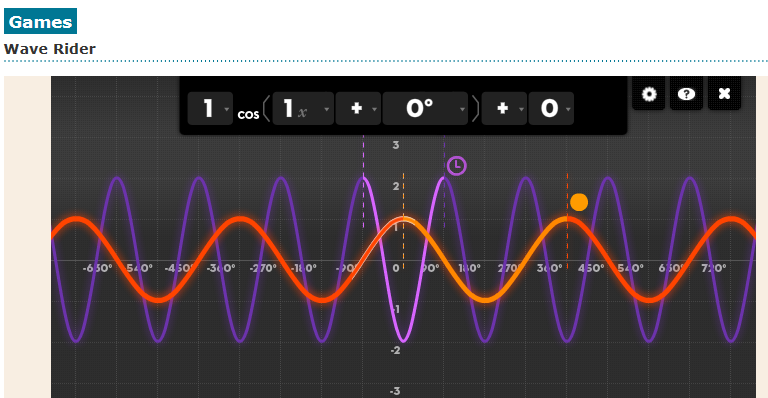
Wave Rider Game
In this game, student must race the timer to write the equation of a sinusoidal function that matches the given graph. Extra point are given if you can collect the token. See who in your class can beat the high score.
http://www.bbc.co.uk/bitesize/higher/games/wave_rider/
![]()
Desmos Sinusoidal Transformations Investigation (Download: SineTransformationsInv.docx)
This investigation assumes that students understand the basic properties of y = sinx and y = cosx and the transformations related to y = a f[b(x - c)] + d. Students will explore how the parameters a, b, c, and d affect sinusoidal functions.
The investigation involves three steps:
1. Use Visualization to predict what characteristics will change when each of the parameters are adjusted.
2. Verify the predictions from step 1 by using Desmos and sliders for each parameter.
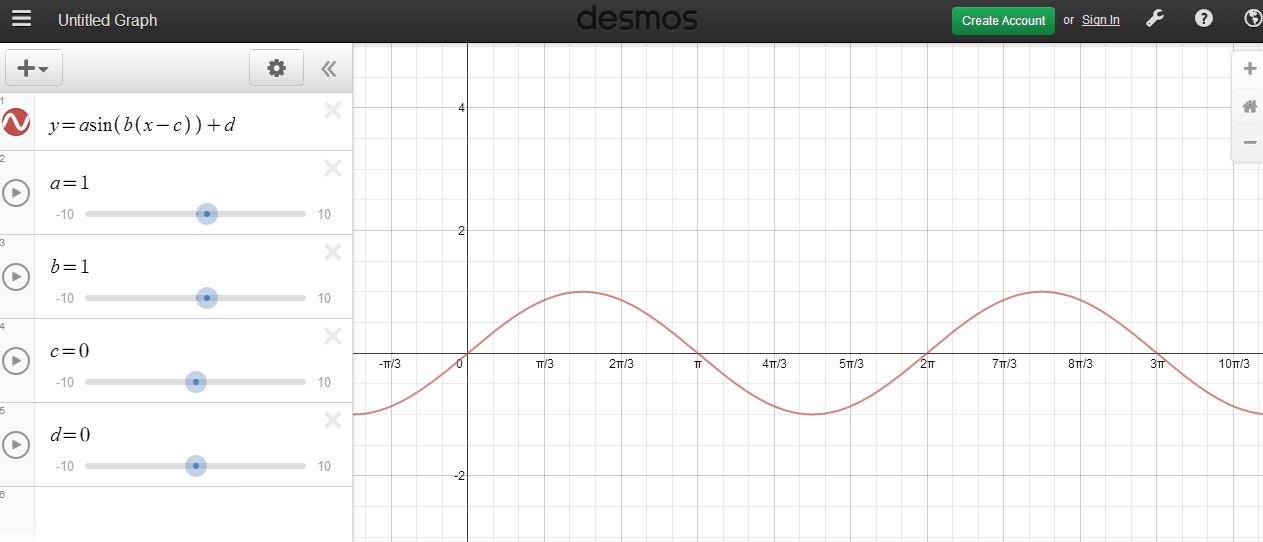
3. Explore in more detail the relationship between the parameters and the characteristics of the graph.
![]()
Investigation - Transformations Connections (Download: TransformationsConnections.docx)
This activity asks students to review a transformation on a function they are already familiar with and then apply the same type of transformation to a sinusoidal function.
This is an example of making Connections between mathematical concepts. Visit the Connections Process Page to explore more ways to incorporate Connections in your teaching.
![]()