EMPL: Operations - Additive Thinking

Operations - Additive Thinking

HOME	VERSION BILINGUE

Click here to report a broken link to a website or a document

Note: Adobe Flash Player is required to view the video.

View the Foundational Webinar "Additive Thinking".

Webinar Slides: click here to open (PDF)

Webinar Guide: click here to open (PDF)

Your feedback is valued!

After watching the archived webinar, please fill out this short survey.

What Is Additive Thinking?

Addition

Students are able to manipulate numbers by joining, separating, and comparing while engaging in flexible mathematical reasoning. It is

a capacity to work flexibly with the concepts, strategies and representations of addition and subtraction as they occur in a wide range of contexts. (mathematical reasoning)
going beyond memorization of basic arithmetic skills
the means to communicate additive understanding effectively in a variety of ways (for example, words, diagrams, symbolic expressions, and written algorithms).

Why Is Additive Thinking Important?

According to research completed by Terezinha Nunes, Peter Bryant, Rossana Barros and Kathy Sylva (2011), both mathematical reasoning and arithmetic skills were predictors of mathematical achievement, however, students’ ability to reason mathematically was the stronger predictor of success. If this is true, then educators must help students progress beyond memorization of arithmetic facts in order to develop mathematical reasoning. Students must be provided with opportunities to explore additive thinking in a variety of contexts and in different ways in order to understand that it is more than just addition and subtraction.

Teacher Background Knowledge

What do I need to know as a teacher in order to be able to teach the concept(s)?

Big Ideas

Once students trust “the count”, they can flexibly manipulate numbers in order to make solving problems easier by

○ using Parts and Wholes

○ decomposing / Recomposing

○ partitioning

○ compensating

○ using Constant Difference

Students use mathematical reasoning to build connections between inverse problems. Addition is not just adding. It’s subtraction as well as it deals with questions where the start, change or result is unknown. It is joining, separating and comparing.
Subtraction is not just “take away”. It is also a comparison (how many more, how many less, what is the difference?).

Vocabulary

Potential Misunderstandings

Mathematics Draft K-4 Curriculum (PDF)

K-9 Program of Studies (PDF)

In the document below, you will find outcomes from the elementary program of studies related to additive thinking as the EMPL team sees it. Other outcomes may be closely related but were not included in this project.

What level of understanding do your students have regarding Additive Thinking? Use the “Big Ideas of Additive Thinking” to guide your teaching. Sample evidence is provided for each Big Idea in order to guide you when assessing your students’ level of understanding.

Additive Thinking - Alberta Students

Alberta students share their strategies for solving addition and subtraction questions. What strategies are they using?

Supporting Struggling Students - Additive Thinking

How do you support students who are struggling with additive thinking? Alberta students struggling with solving questions are guided by the interviewer's questions in order to solve the questions independently. How does the interviewer provide "just in time" support?

What researchers say about additive thinking:

The following is a list of researches and/or articles on operations with a special emphasis on Additive Thinking. Summaries, quotes and references are offered as suggestions to further your professional development on this topic.

This article presents how children learn the basic addition and subtraction facts, why many have difficulty mastering these basic skills, and what teachers can do to prevent or overcome these learning difficulties. "...evidence indicates not only that an understanding of commutativity enables children to learn all basic multiplication combinations by practicing only half of them but also that this conceptual knowledge may also enable a person’s memory to store both combinations as a single representation."

Baroody, A. (2006). Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them. Teaching Children Mathematics, 13(1), 22-31.

Mathematic

This article is about the journey of a grade 2 teacher wanting to ensure students develop an understanding of the basic math facts as per the following NCTM statement: “As children in prekindergarten through grade 2 develop an understanding of whole numbers and the operations of addition and subtraction, instructional attention should focus on strategies for computing with whole numbers so that students develop flexibility and computational fluency. Students will generate a range of interesting and useful strategies for solving computational problems, which should be shared and discussed” (NCTM 2000, p. 35). It describes in detail the addition strategies that students used and mini-units to teach each strategy. Each mini-unit includes an introduction using manipulatives, a student illustration of the strategy, math journaling, and an informational newsletter describing the strategy to parents.

Buchholz, L. (2004). Learning Strategies for Addition and Subtraction Facts: The Road to Fluency and the License to Think. Teaching Children Mathematics, 10(7), 362-367.

This article examines what may be missing in the models we most commonly use and why 10-frame tiles offer an effective alternative to base-10 blocks for teaching place value. The authors further describe how teachers can use the 10-frame model to help children develop understanding of number and place value concepts and skill with computation.

Losq, C. (2005). Number Concepts and Special Needs Students: The Power of Ten-Frame Tiles. Teaching Children Mathematics, 11(6), 310-315

This article presents how applying known facts to derive unknown facts results in efficiency, flexibility, and an understanding of number combinations for young students.

"But what exactly does fluency mean, and how might fluency differ from having instant recall of each and every basic fact? The goal of this article is to examine what it means to be fluent with basic addition facts and to focus on activities that teachers can use to prepare students for fluency. "

Kling, G. (2011). Fluency with Basic Addition. Teaching Children Mathematics,18(2), 80-88.

Quick Assessment Rubric

Quick Assessment

Original version - PDF

Original version - Word

These activities were provided in the Additive Thinking webinar. Choose at least one activity to give to your students. Have them record their responses. Pay special attention to how students get to their answers. Do they use counting or do they use Additive Thinking?

Easter Egg Hunt		The Case of the Hotdogs

Original version - PDF Original version - Word Exemplars - PDF		Original version - PDF Original version - Word Exemplars – PDF

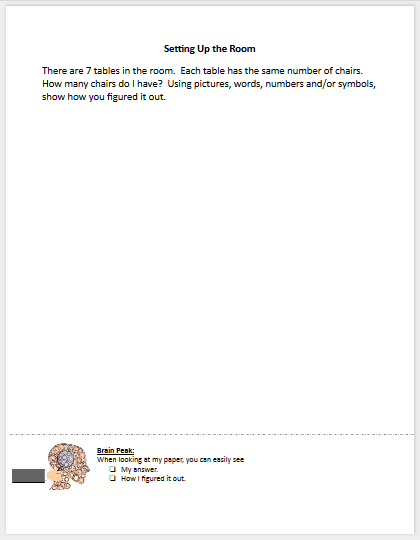
Let's Have a Picnic!		Setting Up the Room

Original version - PDF Original version - Word Exemplars - PDF		Original version - PDF Original version - Word Exemplars - PDF

Programming decisions and the selection of learning resources are made by school authorities, schools, teachers and students.

The use of authorized resources is not mandatory. A broad range of learning resources may be used to meet the needs of all students.

The links below will provide you with a variety of resources that may come in handy when teaching the concept of additive thinking.

These resources are suggestions and are meant to complement what you are already using. They are not necessarily aligned to Alberta Curriculum. These resources come from a variety of sources and are not affiliated with Alberta Education.

Click here to submit a resource

Click here to report a broken link to a website or a document

Click below to learn more about specific strategies

"Trust the Count" mini assessment and teaching activities
"Strategies must be..." poster
Other resources

How many strategies do students need to master?

"Students investigate a variety of strategies, including standard/traditional algorithms, to become proficient in at least one appropriate and efficient strategy that they understand.

Over time, students refine their strategies to increase their accuracy and efficiency." (Alberta Education, pg. 9, 2016)

Parent Letters about the Big Ideas:

The following documents could be sent home as a letter to the parent, in monthly newsletters, etc. in order to support parents in their understanding of the big ideas of Additive Thinking. You could send home a letter in its entirety or split it apart and send home a single question. It is important that parents do not see it as a tool for testing their child’s understanding but as a tool for facilitating conversation.

Big Idea 1

Additive Thinking Big Idea 1